He uses statistics as a drunken man uses lamp posts – for support rather than for illumination. – Andrew Lang

• Our device “improved diagnostic accuracy by more than 50%!”
• Another tool “improved diagnostic accuracy more than 120%!”
• “Our test is 99.4% accurate!”

This all sounds fantastic! But what exactly is accuracy? Recall that,

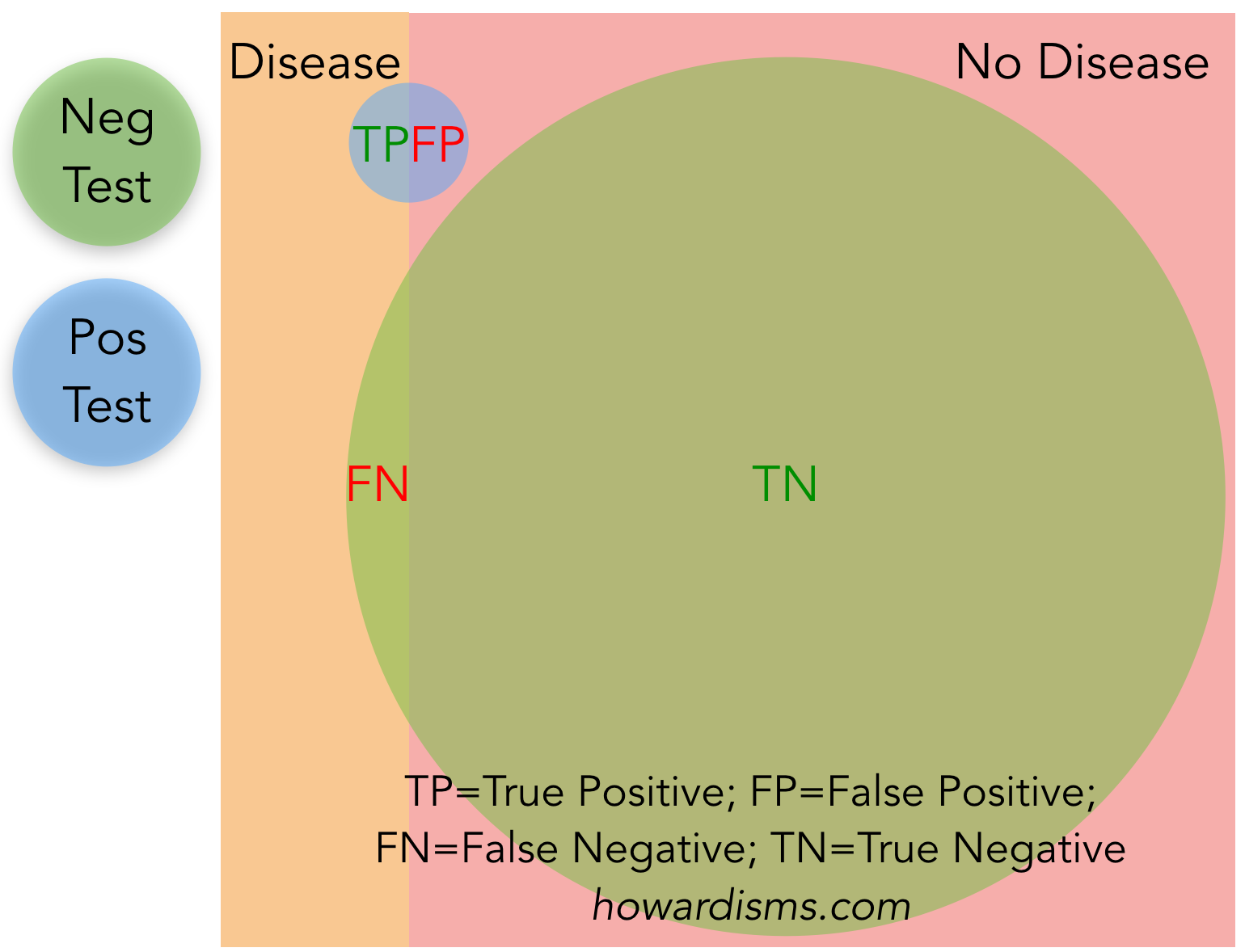
Accuracy = (True Positives+True Negatives)/(True Positives + False Positives + False Negatives + True Negatives).

In other words, accuracy is the total number of true results divided by the total number of results. So imagine that 1 person among 500 has a particular disease. The test fails to detect the person with disease (FN=1) while falsely identifying 2 people as having the disease (FP=2). The other 497 patients are true negatives (TN=497). There are no true positives. What is the accuracy of this test?

Accuracy = (0+497)/(0+2+1+497) or 497/500 = 99.4%!

So, a test with 99.4% accuracy failed to identify the one person with disease and falsely identified two people as having the disease who did not. If it had correctly identified the one person with the disease, it would have been 99.6% accurate, even though 2 out of 3 positive results were false positives. In neither example does the word accuracy mean what we might think it should mean intuitively.

Advertisers and study-authors love the word accuracy. What about the other examples at the conference? Well a test whose accuracy increases from 96% to 98% could be advertised as having improved accuracy by more than 50% (since it reduced inaccuracy by 50%). The wording of such a claim is, in fact, as ambiguous as the word accuracy itself. The word accuracy is a tool for the dishonest.

Stop using the word accuracy and be leery of those who do. 

What about the false positive rate of our imaginary test?

The false positive rate = 1 – specificity or 1 – TN/(TN+FP). In our hypothetical scenario, the false positive rate is 0.4%. That sounds excellent and it is indeed accurate: only two people out of 500 had false positives. But that number is clinically useless and doesn’t tell the real story. We don’t order 500 tests at a time, we order 1 at a time. So when a patient is sitting in front of you with a positive test result, knowing that the false positive rate is 0.4% doesn’t help you tell the patient that her result actually has a 2/3 chance of being falsely positive (nor does the accuracy rate help us understand this).

On the other hand, the positive predictive value (PPV) is helpful. Recall that PPV = TP/(TP+FP) or 1/3 in this case. That number is exactly what you need in order to counsel the patient sitting in front of you with a positive result: She has a 1 in three chance that her test result is accurate.

The Quad Screen test for antenatal Down syndrome screening is an interesting example. The test is designed to have only a 5% false positive rate. This statistic is repeated over and over again in nearly ever description of the test: a 5% false positive rate. Yet, the screen is “positive” at any result which gives a ≥ 1 in 270 chance of Down syndrome. About 97.9% of positive results are false positives. Knowing about the 5% false positive rate doesn’t help you in the least bit interpret a positive test result nor does it help you counsel a patient who might be interested in the test. The 5% false positive rate means that 1 in 20 women who take the test will have a false positive result; by contrast, about 1 in 950 women will have a true positive result. In other words, for every true positive result, there will be about 47.5 false positives, a positive predictive value of only 2.1%.

Stop using the misleading false positive rate and start using positive predictive value instead. 

Maybe this would have been a better quote to start with:

Truth does not consist in minute accuracy of detail, but in conveying a right impression. – Henry Alford