Until I know this sure uncertainty,
I’ll entertain the offered fallacy. – William Shakespeare, The Comedy of Errors
My four year old daughter asked me to guess which two numbers she was thinking of, and all she would tell me is that the two numbers add up to 10. How do I approach this problem? I guess; but my guess is not entirely uninformed.
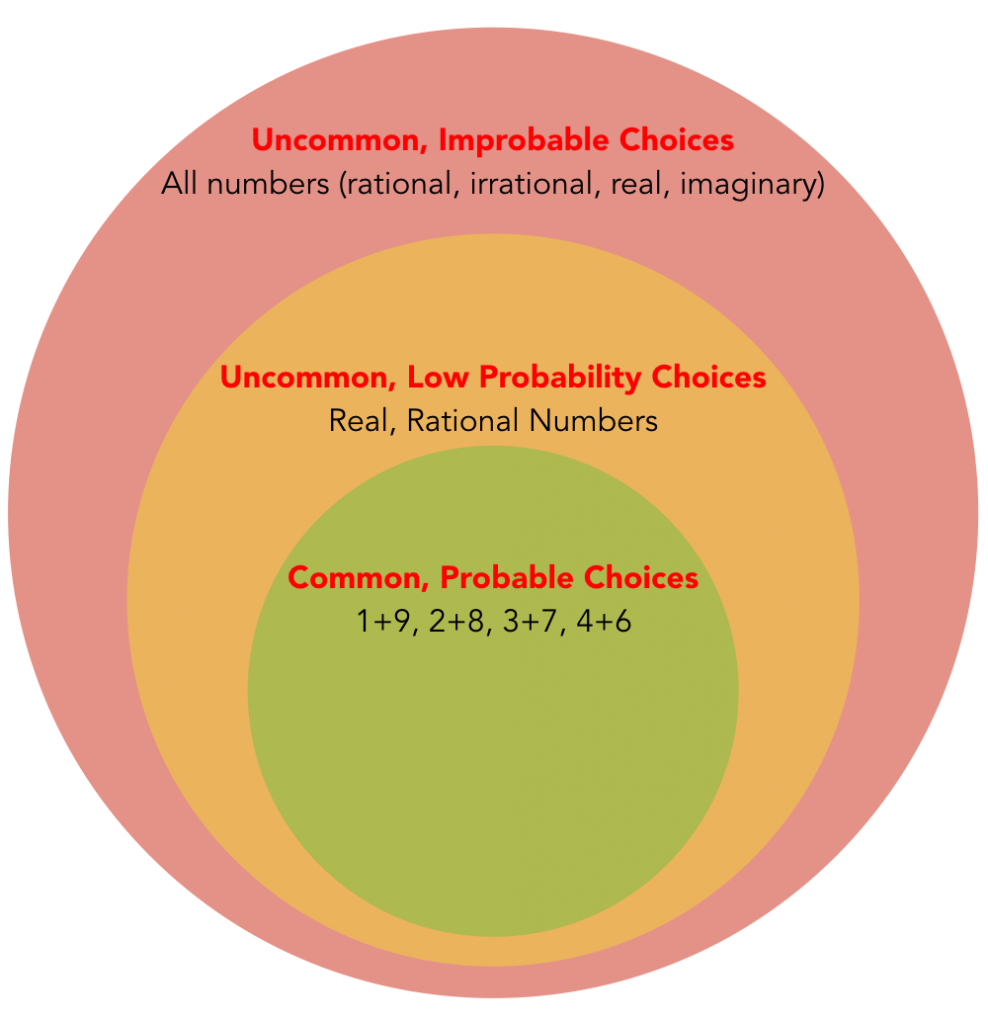
First, I would assume that she is talking about integers. I can also assume that she is talking about positive numbers (she probably doesn’t know much about the concept of negative numbers). She is likely thinking of two different numbers (since that’s how a four year old would process the phrase two numbers), and I doubt she would consider zero (nothing) as a number. This leaves just four likely options: 1+9, 2+8, 3+7, and 4+6. Knowing that people tend to think of numbers in the middle of a sequence, I picked 4+6 (and was right).
Am I psychic? No. Lucky? No. I simply bet on the most probable solution. Yet 42.5 and -32.5 as well as pi + 6.8584 could have been the answers. Even among rational numbers, there are an infinite number of solutions. This is how we make any decision. There is a real answer (whatever is in her head) but without her telling me the answer, I need to use all ascertainable data to make my best guess (that is, the most probable solution). When patients present with a problem, there is an actual diagnosis, but they don’t know it, so we must use all ascertainable data to make a best guess (and change that guess to the new most likely solution when we learn new information).
So what did I do when guessing the two numbers? I divided the infinite number of possible solutions into common solutions with a high probability of being correct, uncommon solutions with a low probability, and uncommon solutions that are improbable.
In other words, I made an exhaustive (infinite!) differential diagnosis once I was presented with the chief complaint (“Daddy, guess two numbers…”). In a real clinical encounter, I would then start asking a series of questions to narrow down my differential diagnosis. Note that the questions I ask are based upon the differential diagnosis, so the differential is very important and must be considered before the questions. For example,
- Are they whole numbers?
- Are they positive numbers?
- Are they two numbers different?
- Are the numbers even or odd?
With each additional bit of information I gather, I quickly narrow down an infinite list. If I can get answers to those four questions (don’t assume we can always get answers), I have narrowed down an infinite number of choices to just two. There is also a possibility that I cannot get certain answers to each question; and this is more the case when dealing with clinical medicine. “Does the x-ray show a pneumonia?” The true answer might be, “There is an 80% chance that the x-ray shows a pneumonia.” Nevertheless, I can still use this information to make one diagnosis more likely (pneumonia) and another less likely (lung cancer).
A test is just another type of question. I can ask my daughter if she is talking about two different numbers; she may not know the answer. I could also perform an experiment. For example, I could have her subtract one number from another and tell me whether the answer is equal to zero. In this same way, I order tests in clinical medicine. A CBC or a CT scan is just another form of interrogation.
In clinical medicine, I like to talk about diagnoses in the same three tier system. I call them horses, zebras, and Tasmanian Tigers. When you hear hoofbeats, think horses. It is true: Common things are common and rare things are rare. Our knowledge of what is common (the accessibility bias) saves us time and makes us efficient; and we are usually correct because common things explain most things. But sometimes hoofbeats are zebras, and sometimes they are Tasmanian Tigers.
Tasmanian tigers officially went extinct in 1936. They were a marsupial that was hunted to extinction in parts of Australia, New Zealand, and Tasmania by farmers and others. Yet, every now and again, someone spots an animal in the wild they believe is a Tasmanian tiger. I have seen zebras and I know where to go find them; but I have never seen a Tasmanian tiger and, as far as I know, I never will. Still, I wouldn’t be shocked if someday another one is spotted deep in the wild bushlands of Australia.

The sum of Tasmanian tigers + zebras + horses is equal to all possible diagnoses. Most of those don’t interest me; but as long as something is possible, it is still on the list. We spend most of our time in the green space of horses, and occasionally we venture off into the goldenrod pasture of zebras. Let’s look at a practical example. Let’s consider a few choices for postmenopausal bleeding.
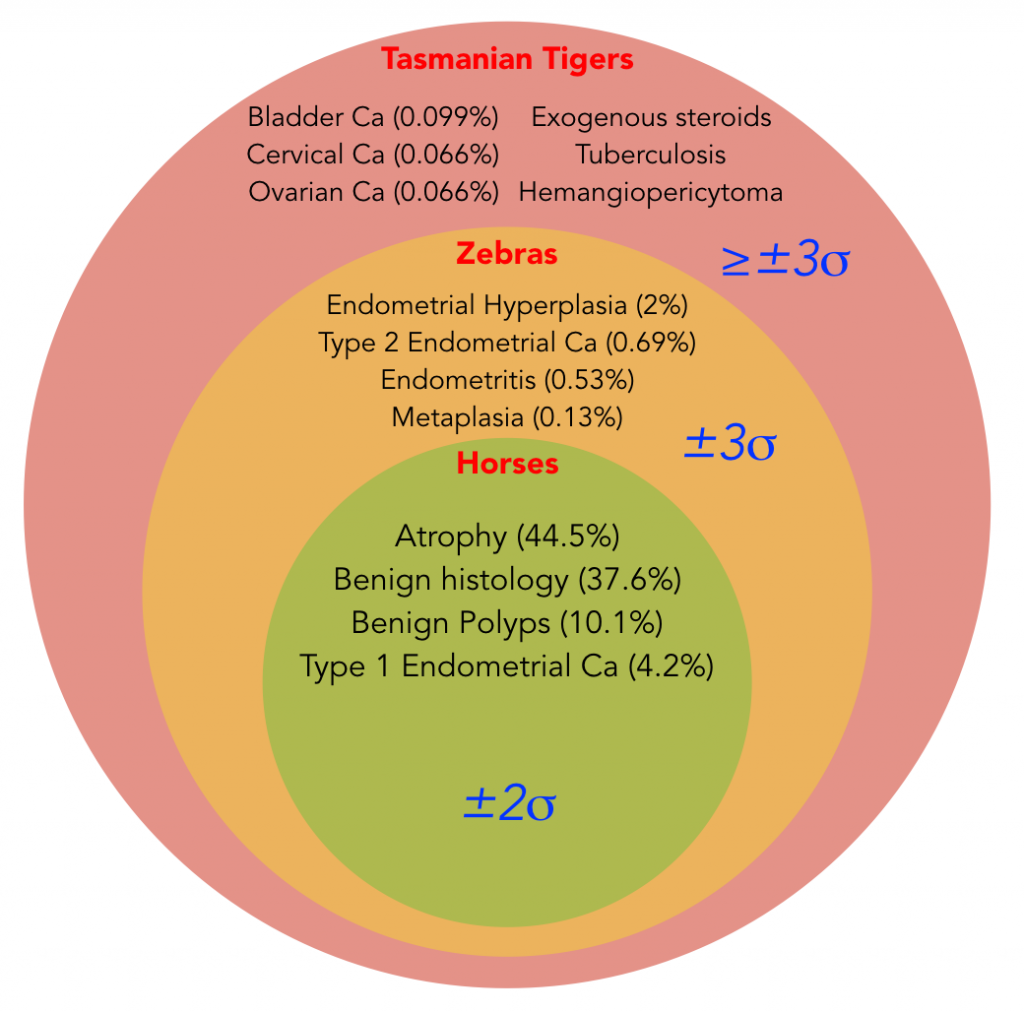 I have arbitrarily (and not accurately) divided this differential diagnosis into three groups based on standard deviations (yes, I know the math isn’t perfect). But the general idea is that about 95% of diagnoses are horses, while about 99.7% of all diagnoses are either horses or zebras. That last 0.3% has a ton of stuff in it, not just the ones I have listed: primary lymphoma of the vagina, hypernephroma, ligneous cervicitis, tamoxifen-affected villous papyraceous, vaginal neurofibromatosis, uterine angiolipoleiomyoma, etc. It even contains so-far undiscovered diagnoses.
I have arbitrarily (and not accurately) divided this differential diagnosis into three groups based on standard deviations (yes, I know the math isn’t perfect). But the general idea is that about 95% of diagnoses are horses, while about 99.7% of all diagnoses are either horses or zebras. That last 0.3% has a ton of stuff in it, not just the ones I have listed: primary lymphoma of the vagina, hypernephroma, ligneous cervicitis, tamoxifen-affected villous papyraceous, vaginal neurofibromatosis, uterine angiolipoleiomyoma, etc. It even contains so-far undiscovered diagnoses.
We spend most of our lives with horses, and occasionally meet zebras. The next patient you see with postmenopausal bleeding, you could just tell her not to worry about it and that it is benign and you would be correct 95% of the time. But some zebras and even Tasmanian tigers are always important to consider (like endometrial, cervical, ovarian, and bladder cancers) . So how can we put all this together in a cogent approach to diagnosis?
- Consider the chief complaint and nothing else (two numbers equalling ten or postmenopausal bleeding).
- Develop a reasonable differential diagnosis (if you didn’t think of villous papyraceous, don’t feel bad). Developing the differential diagnosis before you become biased and boxed-in by more information allows you to think more broadly and prevents many forms of cognitive bias (like availability heuristics).
- Interrogate the patient (this includes history and physical exam, as well as lab tests and imaging as appropriate).
- Order the differential diagnosis into a list of working diagnoses (or even a single diagnosis) based on the probability of each diagnosis.
- Make sure that the “can’t be missed diagnoses” are sufficiently unlikely (for example, perform an ultrasound or endometrial biopsy to lower the probability of endometrial hyperplasia and cancer, even though it is an unlikely diagnosis). Note that not every bad diagnosis needs a test performed to “exclude” it. I don’t want to miss ovarian cancer anymore than I want to miss endometrial cancer in a patient with postmenopausal bleeding; but the risk of ovarian cancer is already sufficiently low (0.066%) that I don’t routinely perform an ultrasound to look at ovaries. The risk of endometrial cancer however (about 5%) is too high to not do further evaluation (like an ultrasound or biopsy) to reduce this risk. Even after a negative ultrasound or endometrial biopsy, there is still a risk of endometrial cancer (both have significant false negative rates), but now the post-test probability (or risk) is similar to the risk of ovarian cancer – so we can stop worrying about it until we have a new reason to worry.
- When new evidence emerges which calls the working diagnosis into question (like a failed response to treatment or new symptoms or test results), consider less likely diagnoses and even previously unconsidered diagnoses (someone out there has a hemangiopericytoma, but consider more common diagnoses first before spending resources on this Tasmanian tiger). Also, and importantly, reconsider previously “excluded” diagnoses. Let’s say that we “ruled out” endometrial cancer with a negative endometrial biopsy, but the patient persists in having bleeding. In that case, a D&C may be the most appropriate next step, because the risk of endometrial cancer in a patient with a negative endometrial biopsy is still higher than the risk of Tasmanian tigers like ovarian cancer. So we sometimes need to do a better test (or even repeat the same test again). This is also a good time to do a literature search and/or read current literature about the symptom. In other words, our System 1 thinking (which thrives in the green and goldenrod circles) has probably failed us, so we need to use a more thorough, System 2 approach to the problem.
That’s it. It works. Try it out. We are always giving patients our best guesses; we need to remember that they are all guesses and as such should be subject to revision as new information comes in. That’s what Bayesian updating is, and the process I have described here is Bayesian probabilistic reasoning. It allows me to give the most accurate answer I can to a variety of questions, ranging from my daughter asking me to guess two numbers to a patient asking me to find out why she has postmenopausal bleeding.